Home

Normal distributions

Definition

An important feature of the standard deviation is that, when the population from which the data arise has a distribution that is approximately "normal" (or Gaussian), the standard deviation helps interpret the data in terms of probability (that is, the probability that two samples of data differ merely by chance variation).

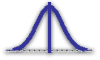
Normal distributions are defined uniquely by two parameters: the mean and the standard deviation of the population.

Normal curves are always symmetrically bell-shaped around the mean. But the steepness or flatness of the bell depends on the standard deviation of the population.